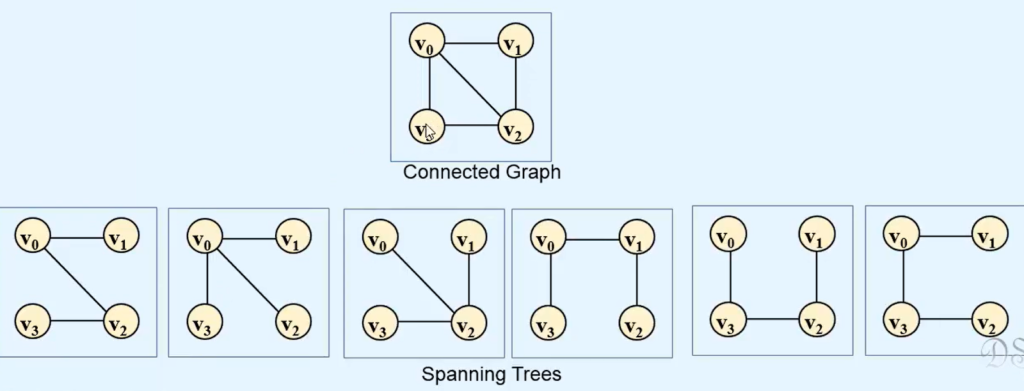
In the fascinating realm of graph theory, one often encounters the concept of a spanning tree—a subgraph that encompasses all the vertices of the original graph while preserving connectivity. However, what happens when the graph is not fully connected, and we can’t form a single spanning tree that covers all vertices? This is where the concept of a spanning forest comes into play.
A spanning forest is a collection of spanning trees, each pertaining to a connected component within the graph. It is a vital construct, offering unique insights into the structure of non-connected graphs. In this article, we will delve into the notion of spanning forests, their significance, and the algorithmic approach to finding them.
The Need for Spanning Forests
Graphs come in various shapes and sizes, and not all of them are guaranteed to be connected. In cases where a graph isn’t connected, attempting to find a single spanning tree that encompasses all vertices becomes an impossibility. Instead, we turn to the concept of a spanning forest.
A spanning forest is essentially a set of spanning trees, with each tree representing a connected component within the original graph. Unlike traditional spanning trees, which are defined in terms of vertices, spanning forests focus on edges. Any vertices that are entirely isolated in the original graph will not appear in the spanning forest.
Non-Connected Graphs with Spanning Forests
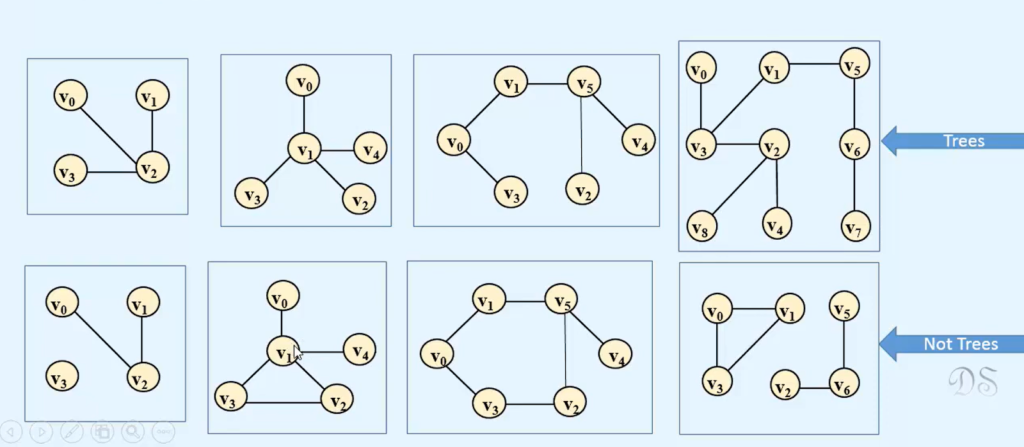
In the realm of graph theory, the absence of connectivity in a graph poses a challenge when attempting to find a spanning tree that covers all its vertices. However, a solution exists in the form of a spanning forest, which consists of multiple spanning trees, one for each connected component within the graph. Unlike traditional connected components, spanning forest components are represented by sets of edges, not vertices. Any isolated vertices within the graph remain absent in the resulting spanning forest.
Constructing a spanning forest is accomplished through the systematic use of the depth-first search algorithm. This process entails repeatedly initiating the algorithm from each unvisited vertex. As this traversal continues, the spanning forest gradually takes shape. Once all vertices associated with edges have been visited, the spanning forest stands complete.
For those interested in implementing this concept, below is a concise C-based representation. The `spanning_forest()` function accepts a graph in edge list format, along with the number of edges (`size`) and vertices (`order`). Additionally, it accommodates a callback function that is invoked with each newly discovered spanning tree. The implementation efficiently employs the `spanning_tree_recursive()` function from the spanning tree algorithm to uncover each individual spanning tree.
#include <stdlib.h>
typedef struct {
unsigned int first;
unsigned int second;
} edge;
typedef void (*treefn)(const unsigned int *, size_t, const edge *, size_t);
void spanning_tree_recursive(const edge *edges, unsigned int size,
unsigned int order, unsigned int *visited, unsigned int *tree,
unsigned int vertex, int edge, unsigned int *len)
{
unsigned int e;
visited[vertex] = 1;
if (edge != -1) {
tree[(*len)++] = edge;
}
for (e = 0; e < size; e++) {
if (edges[e].first == vertex || edges[e].second == vertex) {
unsigned int neighbour = edges[e].first == vertex ?
edges[e].second : edges[e].first;
if (!visited[neighbour]) {
spanning_tree_recursive(edges, size, order, visited, tree,
neighbour, e, len);
}
}
}
}
void spanning_forest(const edge *edges, unsigned int size, unsigned int order,
treefn fun)
{
unsigned int *visited = calloc(order, sizeof(unsigned int));
unsigned int *tree = malloc((order - 1) * sizeof(unsigned int));
unsigned int len, v;
if (visited == NULL || tree == NULL) {
free(visited);
free(tree);
return;
}
for (v = 0; v < order; v++) {
if (!visited[v]) {
len = 0;
spanning_tree_recursive(edges, size, order, visited, tree, v, -1, &len);
if (len > 0) {
fun(tree, len, edges, size);
}
}
}
free(visited);
free(tree);
}Here’s an illustrative program that identifies the spanning forest of the graph depicted above.
#include <stdio.h>
#include <stdlib.h>
/* Connect two edges */
void edge_connect(edge *edges, unsigned int first, unsigned int second,
unsigned int *pos)
{
edges[*pos].first = first;
edges[*pos].second = second;
(*pos)++;
}
void print(const unsigned int *tree, size_t tree_size, const edge *edges, size_t size)
{
unsigned int e;
for (e = 0; e < tree_size; e++) {
printf("(%u, %u) ", edges[tree[e]].first, edges[tree[e]].second);
}
putchar('\n');
}
int main(void)
{
const unsigned int order = 9; /* Vertices */
const unsigned int size = 8; /* Edges */
edge *edges;
edges = malloc(size * sizeof(edge));
if (edges == NULL) {
return 1;
}
/* Square */
edges[0].first = 0;
edges[0].second = 1;
edges[1].first = 1;
edges[1].second = 2;
edges[2].first = 2;
edges[2].second = 3;
edges[3].first = 3;
edges[3].second = 0;
/* Triangle */
edges[4].first = 4;
edges[4].second = 5;
edges[5].first = 5;
edges[5].second = 6;
edges[6].first = 6;
edges[6].second = 4;
/* Line */
edges[7].first = 7;
edges[7].second = 8;
spanning_forest(edges, size, order, print);
free(edges);
return 0;
}The output:
(0, 1) (1, 2) (2, 3)
(4, 5) (5, 6)
(7, 8)Conclusion
Spanning forests are crucial for understanding non-connected graph structures, offering insight into each connected component when a single spanning tree is unfeasible due to lack of connectivity. Using the efficient depth-first search algorithm, we construct spanning forests, revealing the core of each component within the original graph. These forests find applications in network analysis, algorithm design, and other domains, providing a versatile tool to navigate the intricate relationships within graphs, making them indispensable for graph theory enthusiasts and problem solvers. For those interested in delving deeper into algorithmic constructs, our article on hashtables in C offers a comprehensive exploration of data structures, complementing the understanding gained from spanning forests and graph theory.