In the vast realm of computer science, graphs stand out as an essential structure. They model networks, represent relations, and help solve intricate problems. A fundamental concept in graph theory is “connected components.” In this guide, we will dive deep into understanding connected components within a graph and how to identify them using the C programming language.
What are Graphs?
Graphs are like the universe of relationships. Imagine Facebook. Each person is a node, and every friend request is an edge connecting two nodes. But what if we want to find out isolated groups or interconnected subnetworks? Enter connected components!
Connected Components: A Quick Dive
- Definition: A connected component of an undirected graph is a subgraph where any two vertices are connected to each other by paths, and which is connected to no additional vertices in the supergraph;
- Real-World Example: Think of it as islands in an ocean. Each island is self-contained (a connected component), isolated from other islands;
- Significance in C: In the C programming language, managing such structures becomes a combination of data manipulation and logic application, leveraging arrays, pointers, and linked lists.
Visual Representation of Connected Components
Imagine a huge map with different islands (components) surrounded by water (non-connected nodes). These islands can vary in size, with some being a single isolated piece of land and others being massive land masses connected by bridges.
Structuring Graphs in C
To tackle connected components, we first need to structure our graph correctly in C. Let’s dive into the two most common representations:
Adjacency Matrix
- An NxN matrix (N being the number of vertices) where the value M[i][j] is 1 if there’s an edge between vertex i and vertex j;
- Pros: Easy to implement and understand;
- Cons: Consumes more memory especially for sparse graphs.
Adjacency List
- An array of linked lists. The index represents a vertex and each element in its linked list represents the vertices it’s connected to;
- Pros: Saves memory as it only stores connected nodes;
- Cons: A tad bit more complex to implement.
A comparison table to understand the differences:
| Representation | Memory Usage | Implementation Complexity | Look-up Time |
|---|---|---|---|
| Adjacency Matrix | High | Simple | O(1) |
| Adjacency List | Variable | Moderate | O(N) |
Identifying Connected Components in C
We can leverage two well-known graph traversal techniques to identify connected components:
Depth First Search (DFS)
It’s like exploring a maze and taking the first turn you see, and if you hit a dead-end, you retrace your steps. In code, this involves recursion and a visited array.
Breadth First Search (BFS)
Imagine you’re in a room and you shout. The sound spreads in all directions uniformly. BFS works similarly using a queue to track which vertex to visit next.
Remember the golden rule? Always mark visited vertices!
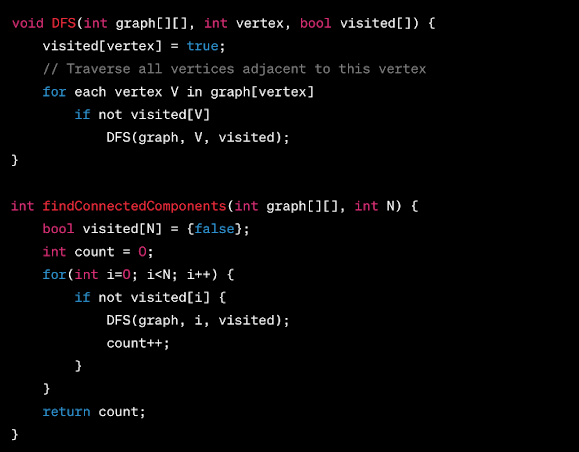
Coding Connected Components in C
Note: This is a pseudocode-like snippet to provide a clear structure.
Applications and Importance
Understanding and implementing connected components can be a game-changer for:
- Social Network Analysis: Identify isolated communities;
- Routing and Navigation: Understand clusters in road networks;
- Biology: Recognize patterns in neural networks or molecular structures.
Pitfalls and Considerations
- Avoid infinite loops. Ensure all nodes are marked as visited;
- Large graphs can lead to stack overflow with DFS. Consider non-recursive approaches or BFS;
- Memory management in C is crucial. Beware of memory leaks!
Choosing the Right Data Structure for Graph Representation
Delving deeper into graph representation in C, it becomes imperative to choose the right data structure based on the specific problem and the operations we expect to perform. Your choice can significantly influence the program’s efficiency.
Factors to Consider:
- Size of the Graph: A large graph with numerous vertices and edges might not be memory efficient with an adjacency matrix due to its fixed size, making the adjacency list a more viable option;
- Frequency of Operations: If you’re often checking for edge existence between nodes, an adjacency matrix provides O(1) lookup time;
- Memory Availability: If memory isn’t a constraint, the adjacency matrix can be more straightforward to work with due to its simple structure.
Recommendations Based on Common Use Cases:
- Social Networks: Given the vast number of users (vertices) but sparse connections (edges), an adjacency list becomes a more efficient choice;
- Transport Systems: In systems like metro or train routes, where connections are more structured and not too vast, an adjacency matrix can be considered.
Here’s a quick comparison table to guide your decision:
| Scenario/Requirement | Suitable Data Structure |
|---|---|
| Large Sparse Graph | Adjacency List |
| Frequent Edge Checks | Adjacency Matrix |
| Memory Not An Issue | Adjacency Matrix |
| Dynamic Graph | Adjacency List |
Conclusion
Connected components serve as the backbone in understanding relationships within graphs. With C as our programming tool, we can efficiently identify and harness these components, offering us profound insights and solutions to intricate problems. With the foundational knowledge and strategies provided, you’re well on your way to mastering connected components in C!
FAQs
A connected graph has all its vertices interconnected. A connected component, however, is a subset of a graph where all its vertices are interconnected but isolated from the rest of the graph.
Absolutely! If a node doesn’t connect to any other node, it stands as its own connected component.
Both can be used efficiently. However, for very large graphs, BFS might be preferred due to potential stack overflows with recursive DFS.
For directed graphs, we have strongly connected components where every vertex can reach every other vertex in the subgraph.
Yes! Given C doesn’t have garbage collection like some languages, programmers should carefully manage memory to avoid leaks.